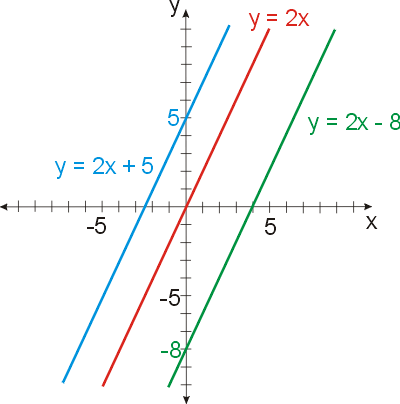Výukové materiály ZŠ Kaplice, Školní 226





| Závislosti | Funkce | Předpis | Lineární | Kvadratické | Nepřímá úměra | Literatura |
Lineární funkce jsou všechny takové funkce, jejichž grafem je přímka. Na zakreslení odpovídající přímky do soustavy souřadnic nám stačí souřadnice dvou bodů.
Není-li zadáno jinak, je definiční obor i obor hodnot množina všech reálných čísel:
D(f) = R
H(f) = R
Předpis lineární funkce je dán obecným vzorcem: y = k . x + q
kde k a q jsou libovolná čísla (koeficienty)
Konstantní funkce je taková funkce, jejíž hodnota se pro žádné x nemění.
y = q
k = 0
q = libovolné
Grafem konstantní funkce je přímka rovnoběžná s osou x. (např: y = 4; y = 0; y = -7)
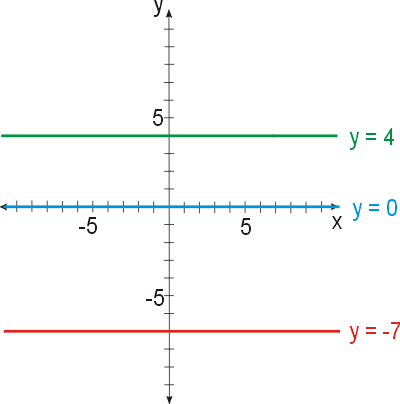
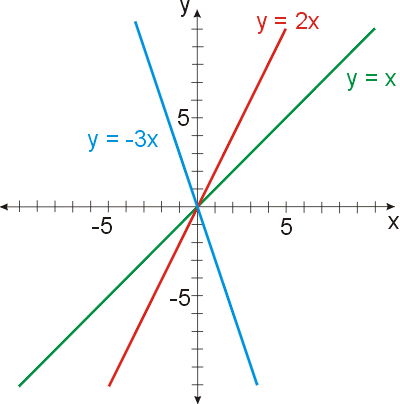
Přímá úměrnost je taková lineární funkce, která má q = 0. Číslu k říkáme směrnice. Čím je k vyšší, tím strměji funkce roste. Pokud je k záporné, funkce klesá.
y = k.x
k = libovolné
q = 0
Grafem konstantní funkce je přímka rovnoběžná s osou x. (např: y = x; y = 2x; y = -3x)
Ostatní lineární funkce vznikají v podstatě posunutím přímé úměrnosti. Číslu q tedy říkáme posunutí. Posunutí určuje, v jakém bodě protne graf osu y
y = k.x + q
k = libovolné
q = libovolné
Grafem konstantní funkce je přímka.