




Výukové materiály ZŠ Kaplice, Školní 226





| úhel | trojúhelník | kružnice v trojúhelníku | čtverec a obdélník | Literatura |
Úhel je část roviny ohraničená dvěma různoběžními polopřímkami. Velikost úhlu měříme úhloměrem. Velikost úhlu se udává ve stupních, minutách a vteřinách. ( Např: 12° 55´ 10´´ = 12 stupňů, 55 minut a 10 vteřin). Jeden stupeň má 60 minut a každá minuta má 60 vteřin.
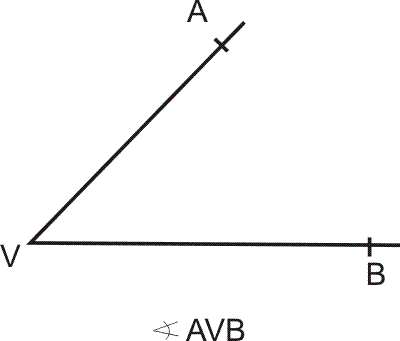
V konstrukcích označujeme úhel třemi písmeny tak, že vrchol úhlu je vždy prostřední písmeno.
Úhel lze také označovat písmeny řecké abecedy. Nejznámější jsou:
| α | alfa | |
| β | beta | |
| γ | gama | |
| δ | delta | |
| ε | epsilon | |
| π | pi | |
| ρ | ró | |
| σ | sigma | |
| τ | tau | |
| ω | omega |
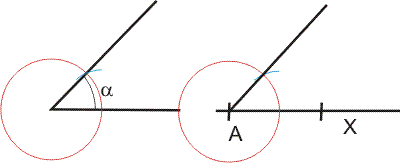
Přenos úhlu na polopřímku AX
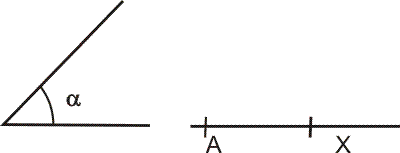
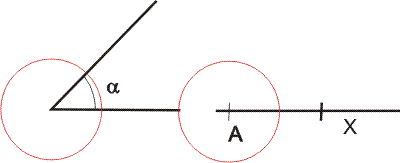
Ve vrcholu úhlu i v bodě A narýsujeme shodnou kružnici.
Kružítkem nabereme vzdálenost mezi průsečíky kružnice a rameny úhlu a přeneseme tuto vzdálenost na kružnici v bodě A.
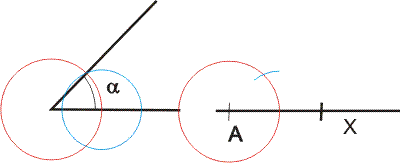
Z bodu A povedeme rameno úhlu průsečíkem kružnic.
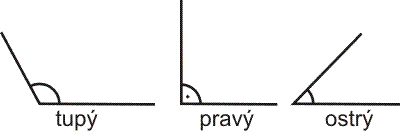
Kolmice na přímku rozdělí polorovinu na dva pravé úhly. Kolmice = pravý úhel = 90° Úhel menší než 90° nazýváme ostrý, úhel větší než 90° nazýváme tupý. Celý kruh odpovídá úhlu 360°, polokruh odpovídá 180° = přímý úhel.
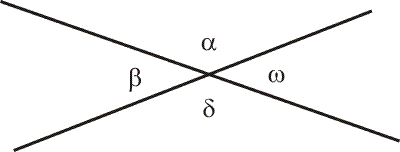
Úhly sousedící na jedné přímce nazýváme vedlejší. Součet jejich velikostí je vždy 180°.
Vedlejší úhly jsou: α a β; δ a ω;
ω a δ; β a δ
Úhly protější nazýváme vrcholové. Jejich velikosti jsou stejné.
Vrcholové úhly jsou: α a δ; β a ω;
Osa úhlu je přímka. Je to množina všech bodů, které jsou od obou ramen stejně daleko. Osa úhel půlí.
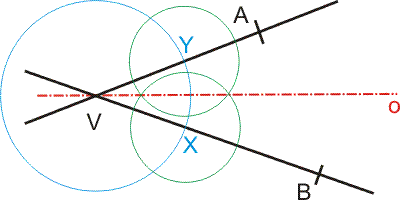
1. Ve vrcholu úhlu sestrojíme libovolnou kružnici.
2. V průsečících kružnice s rameny (X,Y) sestrojíme shodné kružnice.
3. Spojením jejich průsečíků vznikne osa úhlu.