




Výukové materiály ZŠ Kaplice, Školní 226





| čtyřúhelníky | rovnoběžník | lichoběžník | Literatura |
Rovnoběžník je každý čtyřúhelník, který má dvě dvojice rovnoběžných stran.
Při konstrukci rovnoběžníku využíváme některou z těchto základních vlastností:
Sestrojte rovnoběžník ABCD víte-li: |AB| = 5 cm, |AD| = 6 cm, α = 45°.
Rozbor:
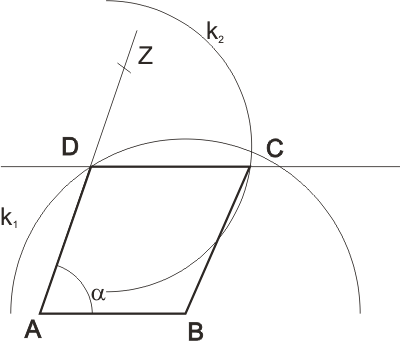
Postup:
| 1) AB; |AB| = 5 cm | (Sestrojíme úsečku AB dlouhou 5 cm) |
| 2) ∠ BAZ; |∠ BAZ| = 45° | (Sestrojíme úhel BAZ o velikosti 45°) |
| 3) k1; k1(A; r = 6 cm) | (Sestrojíme kružnici k1 sestředem v bodě A a poloměrem 6 cm) |
| 4) D; D ∈ k1 ∩ → AZ | (Bod D leží v průsečíku kružnice k1 a polopřímky AZ) |
| 5) p; pIIAB, D ∈ p | (p je rovnoběžka s AB a prochází bodem D) |
| 6) k2; k2(D; r = 5 cm) | (Sestrojíme kružnici k2 sestředem v bodě D a poloměrem 5 cm) |
| 7) C; C ∈ k2 ∩ ↔ p | (Bod C leží v průsečíku kružnice k2 a přímky p) |
| 8) ABCD | (čtyřúhelník ABCD) |
Konstrukce:
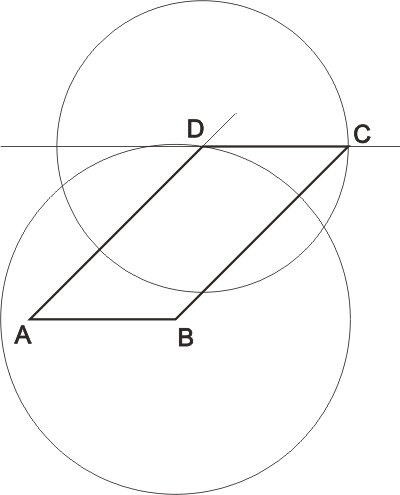
Diskuze:
Úloha má jen jedno řešení. Druhý bod C2( průsečík k2 a p) nevyhovuje zadání
Sestrojte kosočtverec KLMN víte-li: |KL| = 6 cm, vl = 4.
Rozbor:
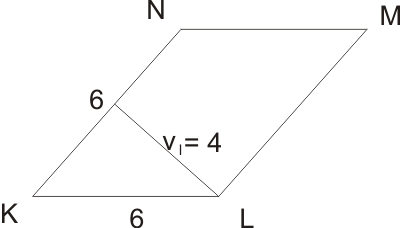
Postup:
| 1) LM; |LM| = 6 cm |
| 2) p1; p1IILM, |pLM| = 4 cm |
| 3) k1; k1(L; r = 6 cm) |
| 4) K; K ∈ k1 ∩ ↔ p |
| 5) k2; k2(K; r = 6 cm) |
| 6) N; N ∈ k2 ∩ ↔ p |
| 7) KLMN |
Konstrukce:
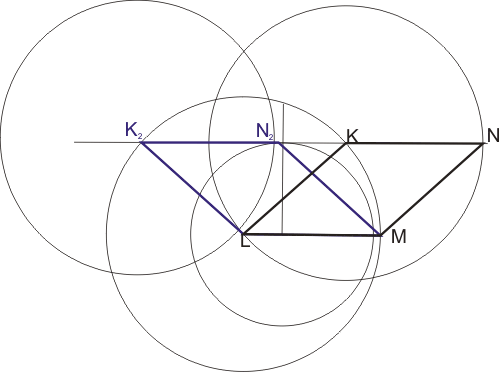
Diskuze:
Úloha má dvě řešení, protože kružnice k1 a přímka p1 mají dva průsečíky K a K2. Oba vzniklé kosočtverce odpovídají zadání.
