Výukové materiály ZŠ Kaplice, Školní 226

Konstrukce čtyřúhelníku

čtyřúhelníky rovnoběžník lichoběžník Literatura

Lichoběžníky

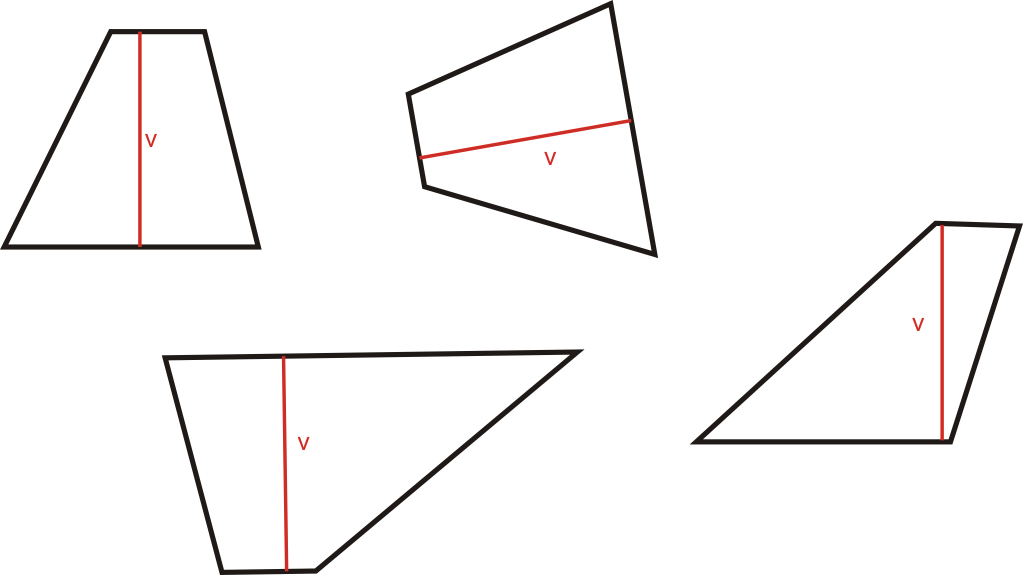
Lichoběžník je každý čtyřúhelník, který má jednu dvojici rovnoběžných stran. Rovnoběžným stranám říkáme základny, druhou dvojici stran nazýváme ramena.

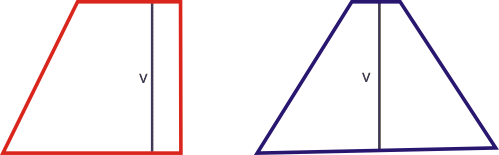
Výška lichoběžníku je vzdálenost základen


Michal Benda CC BY-NC-ND

Speciálními případy lichoběžníků jsou lichoběžník pravoúhlý a lichoběžník rovnoramenný. Pravoúhlý lichoběžník má jedno rameno kolmé na základny. Rovnoramenný lichoběžník má obě ramena i úhlopříčky stejně dlouhé. Je navíc osově souměrný podle os základen.


Michal Benda CC BY-NC-ND

Konstrukce lichoběžníku:

Příklad

Sestrojte lichoběžník ABCD víte-li: |AB| = 6 cm, |AC| = 7 cm, |AD| = 5 cm, ABIICD, |CD| = 3 cm,.

Rozbor:


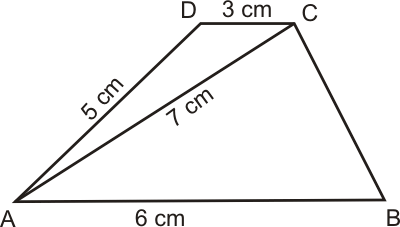
Michal Benda CC BY-NC-ND

Postup:

1) CD;  |CD| = 3 cm
2) k1;  k1(C; r = 7 cm)
3) k2;  k2(D; r = 5 cm)
4) A;  A ∈ k1 ∩ k2
5) p;  pIICD, A ∈ p
6) k3;  k3(A; r = 6 cm)
7) B;  B ∈ k3 ∩ ↔ p
8) ABCD

Konstrukce:


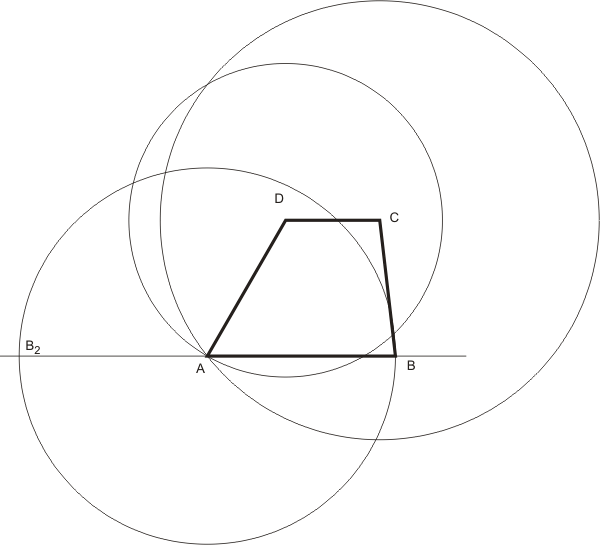
Michal Benda CC BY-NC-ND

Diskuze:

Úloha má jen jedno řešení. Druhý bod B2 nevyhovuje zadání.

 

 

 

Příklad

Sestrojte lichoběžník OPVK víte-li: |OP| = 6 cm, |VK| = 4 cm, |OK| = 5 cm, OPIIVK, v = 3 cm,.

Rozbor:


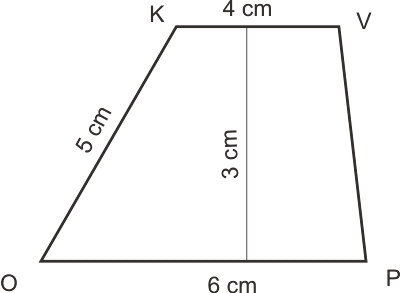
Michal Benda CC BY-NC-ND

Postup:

1) OP;  |OP| = 6 cm
2) p;  pIIOP, |pOP| = 3 cm
3) k1;  k1(O; r = 5 cm)
4) K;  K ∈ k1 ∩ ↔ p
5) k2;  k2(K; r = 4 cm)
6) V;  V ∈ k2 ∩ ↔ p
7) OPVK

Konstrukce:


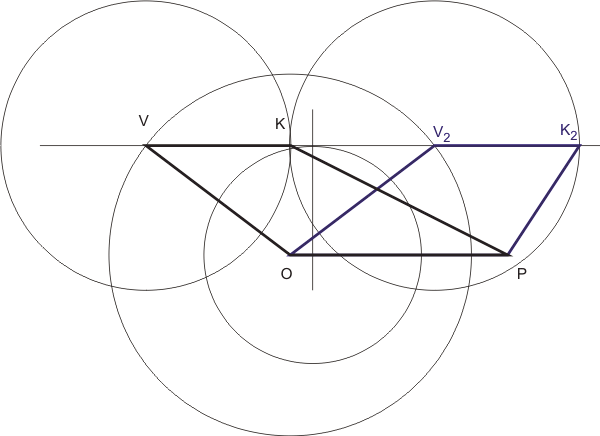
Michal Benda CC BY-NC-ND

Diskuze:

Úloha má dvě řešení, protože kružnice k1 a přímka p1 mají dva průsečíky K a K2. Oba vzniklé lichoběžníky odpovídají zadání.