




Výukové materiály ZŠ Kaplice, Školní 226





| zápis | osa | absolutní hodnota | porovnání | sčítání a odečítání | násobení a dělení | Literatura |
Celá čísla znázorňujeme na ose podobně jako čísla přirozená. Napravo od nuly jsou čísla kladná, nalevo od nuly čísla záporná.
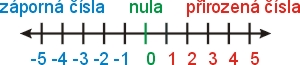
S nulou je potíž. Není ani číslo záporné, ani číslo přirozené (kladné). Proto, chceme-li zdůraznit, že mluvíme o všech kladných číslech včetně nuly, mluvíme o množině nezáporných celých čísel. Naopak, chceme-li všechna čísla záporná s nulou, mluvíme o množině nekladných celých čísel.
Pro správné nakreslení číslené osy platí jistá pravidla. Každá osa musí mít označen počátek (nulu) a musí mít patrné měřítko (označením libovolného dílku). V našem obrázku je to označení čísel nula a jedna. Máme například vyznačit číslo 5. Zakreslíme jej plným kolečkem na správném místě a zapíšeme jeho hodnotu. (viz obr. dole)
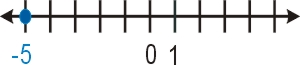
Dvojice čísel, která mají stejnou vzdálenost od nuly, ale na opačnou stranu, nazýváme opačnými čísly. Pro číslo 5 je tedy opačné číslo - 5. Pro číslo - 2 je opačné číslo 2. Opačná čísla mají stejnou absolutní hodnotu.