




Výukové materiály ZŠ Kaplice, Školní 226





| trojúhelník | sinus | cosinus | tangens | Literatura |
Tangens patří do skupiny goniometrických funkcí. V pravoúhlém trojúhelníku je tangens úhlu definován jako poměr přilehlé odvěsny ku protilehlé odvěsně.
Tangens je také definován jako sinus α : cosinus α
| tg x = | sin x |
| cos x |
| úhel | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|---|---|---|
| sinus úhlu | 0 | 1 | 0 | -1 | 0 | |||
| cosinus úhlu | 1 | 0 | -1 | 0 | 1 | |||
| tangens úhlu | 0 | 1 | N | 0 | N | 0 |
Protože nulou nelze dělit, tangens tedy není definován pro úhly, které jsou celými násobky 90° (poloviny π).
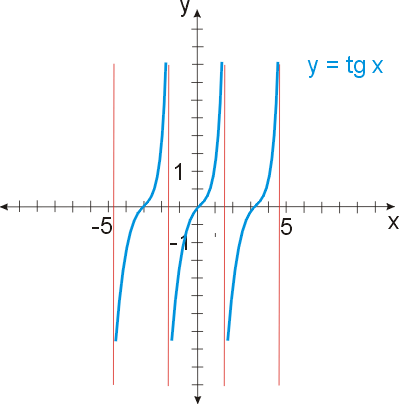
Definiční obor funkce jsou všechna reálná čísla s vyjímkou celých násobků 90° :
D(f) = R - {90° + k•180°} nebo D(f) = R - {0,5π +k•π}.
Oborem hodnot jsou všechna reálná čísla. H(f) = (∞; ∞)
Křivka je souměrná podle počátku soustavy souřadnic [0;0].
Hodnoty se opakují po π (180°).